工作需要,最近接触了一些图像增强的内容。涉及到了一些简单的灰度变换方法,现在作一点总结。
简单起见,本文只考虑单通道灰度图像,同时图片的像素值归一化到 [0 1] 范围内。若要应用于不同灰度范围图像,只需在处理前对图像进行归一,在处理之后进行灰度范围还原即可。这里不作过多讨论。
通俗来说,灰度变换就是找到一种方式(或称为变换函数)$s=T(r)$ ,将图像中所有灰度值为 $r$ 的像素的灰度值变为 $s$,同时保证其像素位置不变。
参考《数字图像处理的MATLAB实现(第2版)》中的介绍个人理解,简单灰度变换方法大体分为两类:1、依据具体的函数形式变换;2、依据灰度分布直方图信息进行变换。更复杂的情况不做讨论。
1. 函数变换形式
以下介绍的各中方法要求所处理的输入图像灰度范围需要保持在 [0 1] 之间。当输出图像灰度范围超出或小于 [0 1] 范围,需要进行归一化,即灰度范围的线性扩展或收缩。
1.1 Gamma 变换
a) 变换公式:
b) 变换曲线:
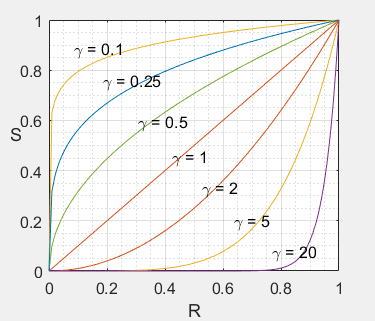
c) 变换说明:
- 当输入范围归一时,输出结果自动归一;
- 参数 $\gamma$ 小于 1 时,扩展低灰度值范围,压缩高灰度值范围;
- 参数 $\gamma$ 大于 1 时,扩展高灰度值范围,压缩低灰度值范围。
1.2 对数变换
a) 变换公式:
b) 变换曲线:
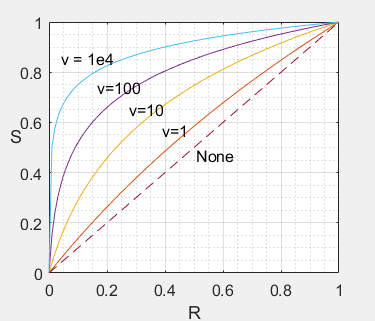
c) 变换说明:
- 当输入范围归一时,输出结果自动归一;
- 对数变换只能扩展低灰度范围,压缩高灰度值范围;
1.3 对比度拉伸
a) 变换公式:
此公式并不能保证变换之后的灰度范围仍充满 [0 1],需要再进行灰度范围的归一。b) 中所画曲线已经是对输出归一化到 [0 1] 区间之后的结果。
b) 变换曲线:
(所有曲线取参数 $m=0.5$ 情况下)
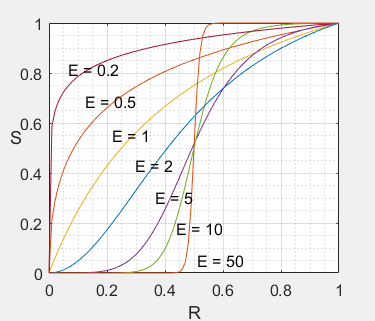
c) 变换说明:
- 输出结果并没有归一,需要额外进行灰度范围的归一化;
- 参数 $m$ 决定了当 $E$ 趋近于正无穷时,使输出灰度值为 0.5 所对应的输入灰度值;
- 此变换在参数 $E$ 取小值时的变换行为明显不同于取较大值时的行为。
1.4 对比度拉伸(采用 Sigmoid 函数进行变换)
通过研究 1.3 中的变换公式,发现其设计的目的主要是为了将输入图像某个中间范围内的灰度范围进行拓展。但是其参数 $E$ 在取小值和大值时的表现并不同,$E$ 取大值时的表现才是设计应达到的目的。进一步发现当 $E$ 取值较大时,曲线与 Sigmoid 曲线类似,何不直接采用 Sigmoid 函数进行灰度变换呢?
a) 变换公式:
此公式并不能保证变换之后的灰度范围仍充满 [0 1],需要再进行灰度范围的归一。b) 中所画曲线已经是对输出归一化到 [0 1] 区间之后的结果。
b) 变换曲线:
(所有曲线取参数 $m=0.5$ 情况下)
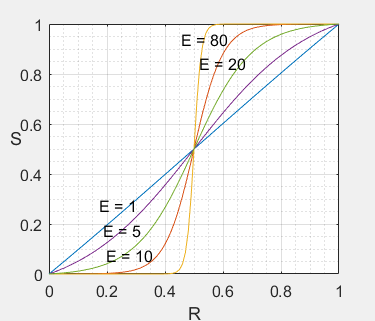
c) 变换说明:
- 输出结果并没有归一,需要额外进行灰度范围的归一化;
- 参数 $m$ 决定了使输出灰度值为 0.5 所对应的输入灰度值;
- 参数 $E$ 取值越大,对中间灰度区间(参数 $m$ 决定)的拉伸,以及高、低灰度区间的压缩越明显。
2. 根据直方图进行灰度值变换
2.1 直方图均衡化
第一次看到直方图均衡化的公式介绍,半天没有反应过来。明白了其中的道理之后发现本质上是一个很简单的事情。以连续分布为例,均衡化的目的本质上是将一个在 [0 1] 范围内的任意灰度分布转换到在 [0 1] 范围内的均匀分布,同时保证在原分布中的像素灰度大小关系在转换之后保持不变。即,如果图像中的任意两个像素 A、B,在灰度转换之前 A 的灰度小于 B,转换之后同样也要保证 A 的灰度小于 B。
设给定输入图像的灰度级的分布,也可以叫概率密度函数(PDF)为 $P_r(r), r \in [0,1]$ ,输出图像的概率密度函数为 $P_s(s), s \in [0,1]$。根据均衡化的定义,要求对任意 $s$,有 $P_s(s)=1$。
对变换来说,自然满足相邻灰度级的像素经过变换之后其灰度级仍然为相邻的:
变换前图像中灰度值从 0 累积到 $r$ 的像素数量应该等于变换后图像中灰度值从 0 累积到 $s$ 的像素数量。如下图z中所示,变换前后的阴影部分,也即各自概率密度积分值相等:
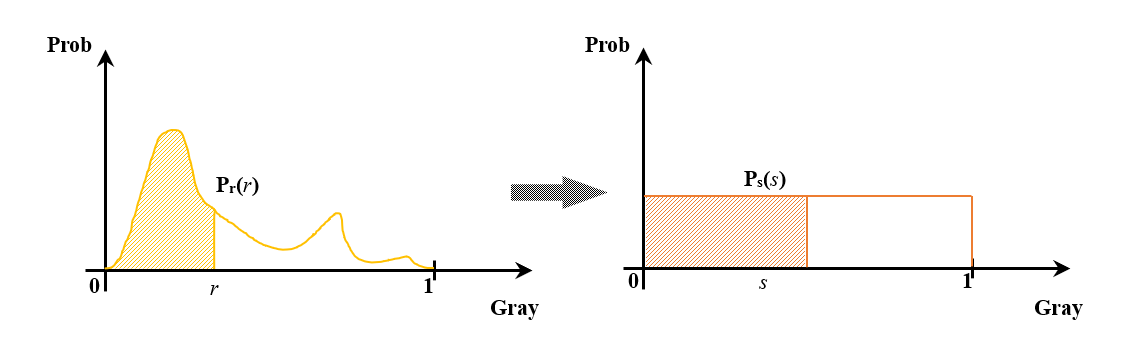
同时注意到 $P_s(s)=1$, 可以得到
此即为直方图均衡化的灰度变化公式,这是一个累积分布函数。它说的是,对原图像中灰度级为 $r$ 的像素,经过均衡化之后,其灰度级变为 $s$,值为原图灰度级的累积分布函数。
2.2 直方图规定化
待续
参考
1: [数字图像处理]灰度变换——反转,对数变换,伽马变换,灰度拉伸,灰度切割,位图切割;
2: 对数及对比度拉伸变换;
3: 对比度调整的各种方法(一);
4: 数字图像处理,经典对比度增强算法;
5: 图像增强之对比度拉伸